今年参加省选，纯属看题 + 感受气氛，虽然不知道明年的自己是否还行走在这条坎坷的路上。
4
11
2015
11
2015
MFOI D1T1 Solve
题目描述
给定 n 和 X0,X1,...,Xn-1，求解 Y0,Y1,...,Yn-1，其中：
f(x) 等于把 x 写成二进制后 1 的个数，比如说：
f(0)=0 , f(1)=1 , f(4)=1 , f(7)=3
其中 表示二进制下的按位异或运算。
请依次输出 Y0,Y1,...,Yn-1 对 取模的结果。
3
27
2015
27
2015
Codeforces #250 Div1 D Child and Sequence(Segment Tree)
D. The Child and Sequence
time limit per test
4 seconds
memory limit per test
256 megabytes
input
standard input
output
standard outputAt the children's day, the child came to Picks's house, and messed his house up. Picks was angry at him. A lot of important things were lost, in particular the favorite sequence of Picks.
Fortunately, Picks remembers how to repair the sequence. Initially he should create an integer array a[1], a[2], ..., a[n]. Then he should perform a sequence of m operations. An operation can be one of the following:
-
Print operation l, r. Picks should write down the value of
. - Modulo operation l, r, x. Picks should perform assignment a[i] = a[i] mod x for each i (l ≤ i ≤ r).
- Set operation k, x. Picks should set the value of a[k] to x (in other words perform an assignment a[k] = x).
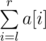Can you help Picks to perform the whole sequence of operations?
3
25
2015
25
2015
THU2013楼房重建calc（Segment Tree）
问题描述
小A的楼房外有一大片施工工地，工地上有N栋待建的楼房。每天，这片工地上的房子拆了又建、建了又拆。他经常无聊地看着窗外发呆，数自己能够看到多少栋房子。
为了简化问题，我们考虑这些事件发生在一个二维平面上。小A在平面上(0,0)点的位置，第i栋楼房可以用一条连接(i,0)和(i,Hi)的线段表示，其中Hi为第i栋楼房的高度。如果这栋楼房上任何一个高度大于0的点与(0,0)的连线没有与之前的线段相交，那么这栋楼房就被认为是可见的。
施工队的建造总共进行了M天。初始时，所有楼房都还没有开始建造，它们的高度均为0。在第i天，建筑队将会将横坐标为Xi的房屋的高度变为Yi(高度可以比原来大---修建，也可以比原来小---拆除，甚至可以保持不变---建筑队这天什么事也没做)。请你帮小A数数每天在建筑队完工之后，他能看到多少栋楼房？
为了简化问题，我们考虑这些事件发生在一个二维平面上。小A在平面上(0,0)点的位置，第i栋楼房可以用一条连接(i,0)和(i,Hi)的线段表示，其中Hi为第i栋楼房的高度。如果这栋楼房上任何一个高度大于0的点与(0,0)的连线没有与之前的线段相交，那么这栋楼房就被认为是可见的。
施工队的建造总共进行了M天。初始时，所有楼房都还没有开始建造，它们的高度均为0。在第i天，建筑队将会将横坐标为Xi的房屋的高度变为Yi(高度可以比原来大---修建，也可以比原来小---拆除，甚至可以保持不变---建筑队这天什么事也没做)。请你帮小A数数每天在建筑队完工之后，他能看到多少栋楼房？
输入格式
第一行两个正整数N,M
接下来M行，每行两个正整数Xi,Yi
接下来M行，每行两个正整数Xi,Yi
输出格式
M行，第i行一个整数表示第i天过后小A能看到的楼房有多少栋
样例输入
3 4
2 4
3 6
1 1000000000
1 1
2 4
3 6
1 1000000000
1 1
样例输出
1
1
1
2
1
1
2
数据约定
对于所有的数据1<=Xi<=N，1<=Yi<=109
3
24
2015
24
2015
今天开始要更新了~
感觉老是在博客上写计划没什么意思，而且写点总结和题解应该也有助于加深印象，所以从今天开始要频繁更新了~
今天听yxj讲了一整天的序列相关，东西真是太多了，我想应该要把这些东西好好消化一下= =
首先是莫队算法。
莫队算法是对于一个长度为n的序列A(A1,A2...An)，m个询问{L,R},回复(AL,AR)中随机取出两个数相同的概率。（题目详情请见BZOJ2038小Z的袜子）
其思想这里不再赘述，请见论文。。。
据说曼哈顿MST实现的现在并不常用了，而分块是比较常用的思想。
复杂度：O(n sqrt(n)log n)
2
26
2015
26
2015
考试题解与反思
T1：统计满足Ai mod Ci != 0且Ai & Ai+1 = 0的序列Ai数量。
Hint:20%的数据 N=10，M=2；另有40%的数据N=50，M=5；剩余的数据N=50，M=15。
Solutions:
20分算法：暴力搜索即可；
60分算法：据说还有暴力方法可以拿到60分。
100分算法：学长推倒出了神奇的矩阵：可以用于表示出对于序列中的第k个元素取i值d[i] = j，j为可行方案数量。
如图所示是一个4*4的该矩阵，横行i表示第k个元素可以取的i值d[i]，纵列表示取d[i]时产生的解的数量，现在要做的实际上是通过这样一个4*4的子矩阵利用Dp求出一个2^m*2^m的矩阵。
