At the children's day, the child came to Picks's house, and messed his house up. Picks was angry at him. A lot of important things were lost, in particular the favorite sequence of Picks.
Fortunately, Picks remembers how to repair the sequence. Initially he should create an integer array a[1], a[2], ..., a[n]. Then he should perform a sequence of m operations. An operation can be one of the following:
-
Print operation l, r. Picks should write down the value of
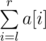 .
. - Modulo operation l, r, x. Picks should perform assignment a[i] = a[i] mod x for each i (l ≤ i ≤ r).
- Set operation k, x. Picks should set the value of a[k] to x (in other words perform an assignment a[k] = x).
Can you help Picks to perform the whole sequence of operations?
The first line of input contains two integer: n, m (1 ≤ n, m ≤ 105). The second line contains n integers, separated by space:a[1], a[2], ..., a[n] (1 ≤ a[i] ≤ 109) — initial value of array elements.
Each of the next m lines begins with a number type 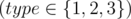 .
.
- If type = 1, there will be two integers more in the line: l, r (1 ≤ l ≤ r ≤ n), which correspond the operation 1.
- If type = 2, there will be three integers more in the line: l, r, x (1 ≤ l ≤ r ≤ n; 1 ≤ x ≤ 109), which correspond the operation 2.
- If type = 3, there will be two integers more in the line: k, x (1 ≤ k ≤ n; 1 ≤ x ≤ 109), which correspond the operation 3.
For each operation 1, please print a line containing the answer. Notice that the answer may exceed the 32-bit integer.
这道题目同时被yxj和vfk讲过的题目,想必是一道神题,仔细一看:裸线段树,咦?操作2是smg?区间取模?没听说过啊,事实上是讲课的时候没太听懂,怎么办?乱搞!考虑和线段树其他区间询问类似的操作,同样也是层层递归下去,走到叶子节点就进行一次取模操作,取模操作今天现学现用(a % b = a - [a/b]*b)。我会说这是我第一次正式地写线段树的题?弄了好久,结果又wa又runtime error一时爽,后来在大神指导下知道了线段树的空间是需要3*数据规模大小的,终于A掉了TAT!改天去学学zkw线段树?
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
using namespace std;
#define maxn 100000 + 5
#define max2 300000 + 5
typedef long long ll;
int n,m,a[maxn],c[max2];ll root[max2];
inline void operation(int t){
root[t] = root[t << 1] + root[t << 1 | 1];
c[t] = max(c[t << 1],c[t << 1 | 1]);
} // t << 1 means the left subree and t << 1 | 1 means the right subtree
inline void updata(int t,int L,int R){
if(L == R) root[t] = c[t] = a[L];
else{
int mid = L + R >> 1;
updata(t << 1, L, mid);
updata(t << 1 | 1, mid + 1, R);
operation(t);
}
}
inline void Set(int t,int l,int r,int x,int y){
if(l == r) root[t] = c[t] = y;
else{
int mid = l + r >> 1;
if(x <= mid) Set(t << 1, l, mid, x, y);
else Set(t << 1 | 1, mid + 1, r, x, y);
operation(t);
}
}
inline void op_mod(int t,int l,int r,int L,int R,int mod){
if(c[t] < mod) return;
if(l == r){
root[t] = c[t] = root[t] - floor(root[t] / mod) * mod;
return;
}
else{
int mid = l + r >> 1;
if(R <= mid) op_mod(t << 1, l, mid, L, R, mod);
else if(L > mid) op_mod(t << 1 | 1, mid + 1, r, L, R, mod);
else{
op_mod(t << 1, l, mid, L, mid, mod);
op_mod(t << 1 | 1,mid + 1, r, mid + 1, R, mod);
}
operation(t);
}
}
inline ll query(int t,int l,int r,int L,int R){
if(l >= L && r <= R) return root[t];
int mid = l + r >> 1;
if(R <= mid) return query(t << 1, l, mid, L, R);
if(L > mid) return query(t << 1 | 1, mid + 1, r, L, R);
return query(t << 1, l, mid, L, mid) + query(t << 1 | 1, mid + 1, r, mid + 1, R);
}
int main(){
int k,L,R,x,y,mod;
scanf("%d%d",&n,&m);
for(int i = 1;i <= n; i++) scanf("%d",&a[i]);
updata(1,1,n);
for(int i = 1;i <= m; i++){
scanf("%d",&k);
if(k == 1){
scanf("%d%d", &L, &R);
printf("%I64d\n",query(1, 1, n, L, R));
}
if(k == 2){
scanf("%d%d%d",&L,&R,&mod);
op_mod(1,1,n,L,R,mod);
}
if(k == 3){
scanf("%d%d",&x,&y);
Set(1,1,n,x,y);
}
}
return 0;
}
2019年2月18日 16:10
An accelerated item and document is initiated for the utilization of the goals for the people. The matter of the success and www.assignmentgeek.com.au is sharply followed for the individuals. The method is inducted for the fluctuations for the parts for the people.
2023年4月23日 19:31
crediblebh