Accelerator‘s Blog

用x = x - t代换题目所给的式子，再用二项式展开，再用-m替换一下，可以得到bm关于am的公式：

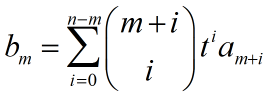
bm=∑nk=mCk−mktk−mak=∑n−mi=0Cim+itiam+i有关ai的通项公式有点令我困惑，里面那个递推式用待定系数法能够解出来，然而加上取模之后我也不知道该怎么办，看了网上的题解，ai的通项公式是这个：

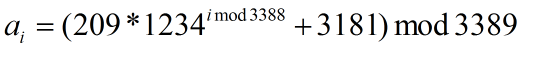
剩下的就没什么好说的了，关于高精度一直就想找一个大整数类的模板，今天看到PoPoQQQ的题解中用的那个操作非常的全，但是那个friend函数不知道干什么的。不过还是把代码贴上来：

#include<cstdlib>
#include<cstdio>
#include<iostream>
#include<cstring>
#include<cmath>
#include<vector>
using namespace std;
#define mod 3389
typedef long long ll;
const ll power_10[] = {1,10,100,1000,10000,100000,1000000,10000000,100000000,1000000000};
struct BigInteger{
    #define BASE 1000000000ll
    long long num[2020];int cnt;
    BigInteger() {}
    BigInteger(long long _){
        memset(num,0,sizeof num);
        num[cnt=1]=_;
    }
    friend istream& operator >> (istream &_,BigInteger &x){
        static char s[3030];
        scanf("%s",s+1);
        int i,len=strlen(s+1);
        for(i=len;i;i--)
            x.num[(len-i)/9+1]+=(s[i]-'0')*power_10[(len-i)%9];
        x.cnt=len/9+1;
        return _;
    }
	BigInteger& operator += (const BigInteger &x){
        int i;
        cnt=max(cnt,x.cnt);
        for(i=1;i<=cnt;i++)
        {
            num[i]+=x.num[i];
            if(num[i]>=BASE)
                num[i]-=BASE,num[i+1]++;
        }
        if(num[cnt+1]) ++cnt;
        return *this;
    }
    friend BigInteger operator + (const BigInteger &x,const BigInteger &y){
        BigInteger re;
        re=x;re+=y;return re;
    }
    friend int operator - (const BigInteger &x,const BigInteger &y){
        int i;
        long long re=0;
        for(i=x.cnt;i;i--)
            (re*=BASE)+=x.num[i]-y.num[i];
        return re;
    }
    friend BigInteger operator - (const BigInteger &x,int y){
        BigInteger re;
        int i;
        re=x;re.num[1]-=y;
        for(i=1;re.num[i]<0;i++)
            re.num[i] +=BASE,re.num[i+1]--;
        while(!re.num[re.cnt])
            re.cnt--;
        return re;
    }
    friend BigInteger operator * (const BigInteger &x,const BigInteger &y){
        BigInteger re(0);
        int i,j;
        for(i=1;i<=x.cnt;i++)
            for(j=1;j<=y.cnt;j++)
            {
                re.num[i+j-1]+=x.num[i]*y.num[j];
                if(re.num[i+j-1]>=BASE)
                    re.num[i+j]+=re.num[i+j-1]/BASE,re.num[i+j-1]%=BASE;
            }
        re.cnt=x.cnt+y.cnt;
        if(!re.num[re.cnt])
            re.cnt--;
        return re;
    }
    BigInteger& operator *= (const BigInteger &x){
        return *this=*this*x;
    }
    BigInteger& operator /= (int x){
        int i;
        for(i=cnt;i;i--)
            num[i-1]+=(num[i]%x)*BASE,num[i]/=x;
        num[0]=0;
        if(!num[cnt])
            --cnt;
        return *this;
    }
    int operator % (int x) const{
        int i;
        long long re=0;
        for(i=cnt;i;i--)
            ((re*=BASE)+=num[i])%=x;
        return re;
    }
    friend ostream& operator << (ostream &_,BigInteger &x){
        int i;
        while( x.cnt>0 && !x.num[x.cnt] )
            --x.cnt;
        printf("%d",(int)x.num[x.cnt]);
        for(i=x.cnt-1;i>0;i--)
            printf("%09d",(int)x.num[i]);
        return _;
    }
}n,m,ans,k = 1,tp = 1;

inline int qpow(int a,int b){
	int ret = 1;
	while(b){
		if(b & 1)ret *= a,ret %= mod;
		a *= a, a %= mod;
		b >>= 1;
	}
	return (ret + mod) % mod;
}
inline int geta(BigInteger x){
	int power = x % 3388 ;
	return (209*qpow(1234,power) + 3181) % mod;
}

int main(){
	int tmp,t;
	cin >> n >> t >> m;
	tmp = n - m;
	for(int i = 0;i <= tmp; i++){
		if(i){
			k *= m + i,k /= i;
			tp *= t;
		}
		ans += k*tp*geta(m + i);
	}
	cout << ans << endl;
	return 0;
}