
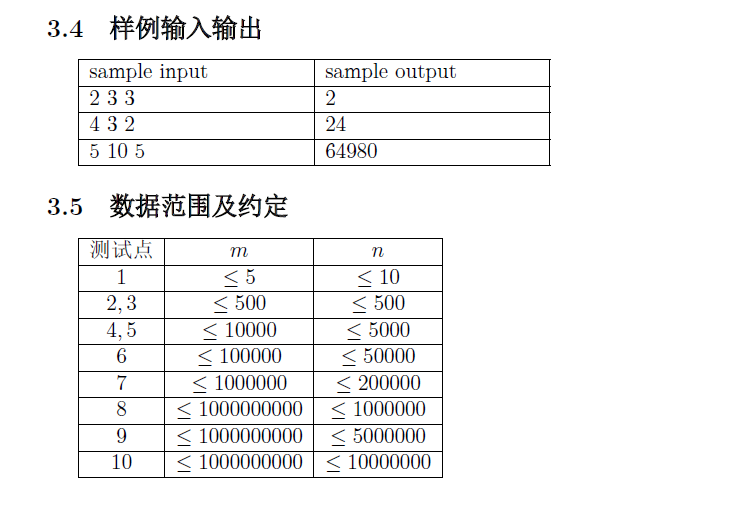
Upd:解释一下。。即求有多少个串,使得每一个串长n, 且这个串中 字符相同的段 的 最大长度 为k。。。
Upd:样例1:可以都用第一种字符也可以都用第二种字符,ans=2
题解:
这种题还是做少了,为毛总是想不到dp~!
30pt DP:F[i][j]表示前i个最长同色位置为j的方案数,用区间dp那一套搞就行了,复杂度O(n^3);
100pt DP:考虑F[i]为最长同色串<=x的方案数,那么F[i] = ΣF[i-j],j = 1→x;由于询问的k是一段区间内的方案,考虑维护前缀和,这样复杂度就变为O(n)了~;
UPD:注意对于样例1那种情况要判一下~
代码:
#include<cstdlib>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long ll;
const int maxn = (1e7) + 5,mod = (1e9) + 7;
int m,n,k,f[maxn],ans;
inline int Inc(int a,int b){return a + b - (a + b >= mod ? mod : 0);}
inline int getpre(int kp){
f[0] = 1;
for(int i = 1;i <= n; i++){
if(i == 1)f[i] = m; //for the 1st case
else if(i <= kp) f[i] = (int) (((ll)f[i - 1]*(m - 1) + 1) % mod);
else f[i] = (ll)(m - 1)*(f[i - 1] - f[i - kp - 1] + mod) % mod;
f[i] = (f[i - 1] + f[i]) % mod;
}
return (f[n] - f[n - 1] + mod) % mod;
}
int main(){
scanf("%d%d%d",&m,&n,&k);
printf("%d",(getpre(k) - getpre(k - 1) + mod) % mod);
return 0;
}
被虐了TAT,今天的MFOI感觉和昨天一样只看懂一道题的题解,此题题意差评(或者说博主语文差评TAT?)。
 评论 (0)
评论 (0)